When you build a structure, if the foundation of that structure is not sound and plum, the structure will not be sound.
About 15 years of effort has yielded both a proof of high level financial reporting semantics and an implementation of those semantics, the logic of a financial report, in the XBRL technical syntax. (Click the image below for a lager view)
This proof allows for many things. First, the proof can be used to evaluate important XBRL taxonomies such as US GAAP, IFRS, UK GAAP, Australian IFRS, and others. My analysis shows taxonomy creation errors, taxonomy creation inconsistencies, and obvious missing pieces.
Second, the proof can help accountants understand and communicate about financial accounting, reporting, auditing, and analysis more effectively and precisely. Fundamentally, all financial reporting schemes have the same foundation, see the Essence of Accounting.
Third, the proof can help you understand how to effectively convey information using the XBRL technical syntax. For example, consider these different representations of exactly the same information: (i.e. each Inline XBRL report looks 100% the same)
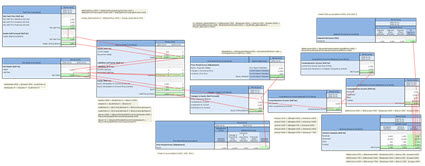
- Reference Implementation: This is the basic reference implementation of the proof. Note the organization and the abstract concepts that help organize the report model. (all information)
- Reference Implementation Removing Abstract Concepts: This is the same facts as the first report but abstract concepts were not used to help organize the report model. The report is just a little harder to read but not that different. (all information)
- Reference Implementation Removing Unnecessary Hypercubes: This report is also the same as the first but in addition to removing the abstract concepts, I also removed all hypercubes that are not required. Again, the report does not look that different. (all information)
- Reference Implementation Combining Hypercubes and Networks: This report is likewise the same as the first but in addition to removing abstract concepts and hypercubes, I combined information within networks somewhat arbitrarily where the combination caused no conflicts. As you can see by looking at the report, it becomes harder to understand and sometimes even confusing. (all information)
What is my point? Well, there are several points. First, each Inline XBRL report looks identical. Second, whether you include or exclude an abstract concept is a preference. Third, whether you use a hypercube in some cases is a preference but other times hypercubes are REQUIRED because you must add noncore dimensions and that can only be done when you use a hypercube. Finally, how you organize information into networks is sometimes a preference, but other times you simply cannot combined disclosed information because conflicts would occur (i.e. that is WHY networks exist, to avoid those information conflicts).
While using things that are preferences can yield elegant looking XBRL-based financial reports and not using them can yield ugly and hard to read reports; these preferences do not impact the meaning conveyed by the XBRL-based financial report.
But being logical is not a preference or a subjective decision. Being logical is objective and can be measured. For example, these rules related to mathematical relationships in each of the four reports yield the exact same verification results in any of the four reports shown above. That proves that the logic of the report does not change when you do, or do not, add abstract concepts or certain hypercubes or put a disclosure in one network as opposed to some other network.
No one really disputes these high level financial report sematics. No one can really dispute the XBRL-based representation of those semantics either; simply running the reports through an XBRL processor and XBRL formula processor indicates whether something is consistent or inconsistent with the XBRL technical specification.
You can have a preference for whether you want to represent a prior period adjustment using one of the two approaches I provide in this PROOF. You can even perhaps create another way to represent that same disclosure and prove that your new way also works. You can prove that your new approach interacts with each and every other piece of a report.
But you cannot dispute the fact that the PROOF works and is consistent with the rules of accounting.
##################################